Design a new rigid pavement for a major interstate highway using the following conditions (four lanes each direction):
| Pavement location | Urban |
|---|---|
| Pavement functional classification | Interstate |
| Number of lanes | 3 lanes in each direction |
| Traffic distribution | Assume 80% of the loading occurs in the design lane |
| Annual growth rate | Assume 2% |
| Design period | Investigate 20, 30 and 40 year design periods |
| Construction Materials | PCC Ec = 31,026 MPa (4,500,000 psi) PCC S’c = 5.17 MPa (750 psi) |
| Load Transfer | Use dowel bars and assume J = 3.2 |
| Overall serviceability loss | po – pt = 4.5 – 3.0 = 1.5 |
| Reliability | Investigate three levels: R = 90%, R = 95%, R = 99%. This represents a typical range of reliability levels encountered for Interstate highways. |
| o | 0.40 |
| Drainage coefficient (Cd) | 1.0 (usually assumed if no better data exist) |
| Loss of support | 1.0 |
| Traffic count | Single unit trucks (assume 0.34 ESALs per truck) = 1872/day Double unit trucks (assume 1.00 ESALs per truck) = 1762/day Truck trains – trucks with more than 2 units (assume 2.60 ESALs per truck) = 247/day |
Design ESALs
The standard multiplier to calculate compound growth is:
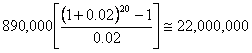
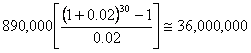
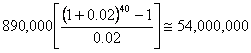
Calculate the Effective Modulus of Subgrade Reaction (k)
This calculation is a multi-step process In the 1993 AASHTO Guide for Design of Pavement Structures. Basically, the steps are as follows:
- Determine the roadbed resilient modulus and the subbase elastic modulus and use these values along with a projected slab thickness to graphically determine a “composite modulus of subgrade reaction” (k:).
- Modify this k: to account for the effects of a rigid foundation near the surface. The idea here is that the subgrade will offer greater support if a rigid foundation (such as bedrock) is located very near the surface.
- Determine how this modified composite modulus of subgrade reaction (or “k-value”) varies throughout a typical year. Typically this is done by season or by month.
- Using a projected slab thickness and a modulus of subgrade reaction that has been modified to account for the effects of a rigid foundation near the surface, use a graph to determine the relative influence the various k-values throughout the year will have on pavement performance. Lower values of k, indicating less support, are potentially more damaging than higher values of k, indicating more support. Therefore, lower values of k are weighted more heavily in determining the weighted average.
- Correct the weighted average k-value to account for the potential loss of support arising from subbase erosion. Subbase materials that are more prone to eroding will result in a larger downward correction to the k-value determined in step 4.
The 1993 AASHTO Guide for Design of Pavement Structures and its associated graphs are needed to carry out this procedure because most steps involve graphical solutions. Although these graphs are not reproduced here, a summary results table is shown below.
| Month | MR | Subbase MR | Composite k | Relative Damage (ur) |
|---|---|---|---|---|
| January | 86 MPa (12,500 psi) | 3,447 MPa (500,000 psi) | 950 | 95 |
| February | 86 MPa (12,500 psi) | 3,447 MPa (500,000 psi) | 950 | 95 |
| March | 86 MPa (12,500 psi) | 3,447 MPa (500,000 psi) | 950 | 95 |
| April | 86 MPa (12,500 psi) | 3,447 MPa (500,000 psi) | 1,000 | 92 |
| May | 103 MPa (15,000 psi) | 3,447 MPa (500,000 psi) | 1,000 | 92 |
| June | 103 MPa (15,000 psi) | 3,447 MPa (500,000 psi) | 1,000 | 92 |
| July | 103 MPa (15,000 psi) | 3,447 MPa (500,000 psi) | 1,000 | 92 |
| August | 103 MPa (15,000 psi) | 3,447 MPa (500,000 psi) | 1,000 | 92 |
| September | 103 MPa (15,000 psi) | 3,447 MPa (500,000 psi) | 1,000 | 92 |
| October | 103 MPa (15,000 psi) | 3,447 MPa (500,000 psi) | 950 | 92 |
| November | 86 MPa (12,500 psi) | 3,447 MPa (500,000 psi) | 950 | 95 |
| December | 86 MPa (12,500 psi) | 3,447 MPa (500,000 psi) | 950 | 95 |
| average relative damage | = | 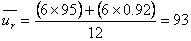 |
Based on Figure 3.5 in the 1993 AASHTO Guide for Design of Pavement Structures, k ˜ 980.
Based on Figure 3.6 in the 1993 AASHTO Guide for Design of Pavement Structures a Loss of Support = 1.0 results in keff ˜ 250.
Use the 1993 AASHTO Empirical Equation
Using the previously calculated ESAL results and the 1993 AASHTO empirical rigid pavement design equation the following pavement thickness designs can be calculated:
| Design Period | Design Period ESALs | Pavement Layer | Layer Thickness | ||
| Reliability = 90% | Reliability = 95% | Reliability = 99% | |||
| 20 years | 22,000,000 | PCC Surface Course | 280 mm (11 inches) |
305 mm (12 inches) |
330 mm (13 inches) |
| HMA Base Course | 100 mm (4 inches) |
100 mm (4 inches) |
100 mm (4 inches) |
||
| Crushed Stone Subbase Course | 135 mm (5.4 inches) |
135 mm (5.4 inches) |
135 mm (5.4 inches) |
||
| 30 years | 36,000,000 | PCC Surface Course | 305 mm (12 inches) |
320 mm (12.5 inches) |
355 mm (14 inches) |
| HMA Base Course | 100 mm (4 inches) |
100 mm (4 inches) |
100 mm (4 inches) |
||
| Crushed Stone Subbase Course | 135 mm (5.4 inches) |
135 mm (5.4 inches) |
135 mm (5.4 inches) |
||
| 40 years | 54,000,000 | PCC Surface Course | 330 mm (13 inches) |
345 mm (13.5 inches) |
380 mm (15 inches) |
| HMA Base Course | 100 mm (4 inches) |
100 mm (4 inches) |
100 mm (4 inches) |
||
| Crushed Stone Subbase Course | 135 mm (5.4 inches) |
135 mm (5.4 inches) |
135 mm (5.4 inches) |
||
In this particular example, which only shows one set of possible solutions, the HMA base course and crushed stone subbase course layer depths were kept constant and the PCC surface course depth was varied depending upon requirements. Notice that a change in reliability level from 90% to 99% results in a PCC slab thickness increase of about 50 mm (2 inches). The 380 mm (15 inch) thick slab shown for the 40-year design (99% reliability) is probably near the maximum practical slab thickness for highway pavements.
