Empirical equations are used to relate observed or measurable phenomena (pavement characteristics) with outcomes (pavement performance). This article presents the 1993 AASHTO Guide basic design equation for flexible pavements. This empirical equation is widely used and has the following form:
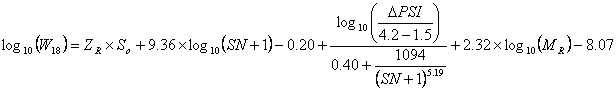
(these variables will be further explained in the Inputs section)
| where: | W18 | equals | predicted number of 80 kN (18,000 lb.) ESALs |
| ZR | equals | standard normal deviate | |
| So | equals | combined standard error of the traffic prediction and performance prediction | |
| SN | equals | Structural Number (an index that is indicative of the total pavement thickness required) | |
| equals | a1D1 + a2D2m2 + a3D3m3+…ai = ithlayer coefficientDi = ithlayer thickness (inches)mi = ith layer drainage coefficient | ||
| ΔPSI | equals | difference between the initial design serviceability index, po, and the design terminal serviceability index, pt | |
| MR | equals | subgrade resilient modulus (in psi) |
This equation is not the only empirical equation available but it does give a good sense of what an empirical equation looks like, what factors it considers and how empirical observations are incorporated into an empirical equation. The rest of this section will discuss the specific assumptions, inputs and outputs associated with the 1993 AASHTO Guide flexible pavement empirical design equation. The following subsections discuss:
- Assumptions
- Inputs
- Outputs
Assumptions
From the AASHO Road Test, equations were developed which related loss in serviceability, traffic, and pavement thickness. Because they were developed for the specific conditions of the AASHO Road Test, these equations have some significant limitations:
- The equations were developed based on the specific pavement materials and roadbed soil present at the AASHO Road Test.
- The equations were developed based on the environment at the AASHO Road Test only.
- The equations are based on an accelerated two-year testing period rather than a longer, more typical 20+ year pavement life. Therefore, environmental factors were difficult if not impossible to extrapolate out to a longer period.
- The loads used to develop the equations were operating vehicles with identical axle loads and configurations, as opposed to mixed traffic.
In order to apply the equations developed as a result of the AASHO Road Test, some basic assumptions are needed:
- The characterization of subgrade support may be extended to other subgrade soils by an abstract soil support scale.
- Loading can be applied to mixed traffic by use of ESALs.
- Material characterizations may be applied to other surfaces, bases, and subbases by assigning appropriate layer coefficients.
- The accelerated testing done at the AASHO Road Test (2-year period) can be extended to a longer design period.
When using the 1993 AASHTO Guide empirical equation or any other empirical equation, it is extremely important to know the equation’s limitations and basic assumptions. Otherwise, it is quite easy to use an equation with conditions and materials for which it was never intended. This can lead to invalid results at the least and incorrect results at the worst.
Inputs
The 1993 AASHTO Guide equation requires a number of inputs related to loads, pavement structure and subgrade support. These inputs are:
- The predicted loading. The predicted loading is simply the predicted number of 80 kN (18,000 lb.) ESALs that the pavement will experience over its design lifetime.
- Reliability. The reliability of the pavement design-performance process is the probability that a pavement section designed using the process will perform satisfactorily over the traffic and environmental conditions for the design period (AASHTO, 1993[1]). In other words, there must be some assurance that a pavement will perform as intended given variability in such things as construction, environment and materials. The ZR and So variables account for reliability.
- Pavement structure. The pavement structure is characterized by the Structural Number (SN). The Structural Number is an abstract number expressing the structural strength of a pavement required for given combinations of soil support (MR), total traffic expressed in ESALs, terminal serviceability and environment. The Structural Number is converted to actual layer thicknesses (e.g., 150 mm (6 inches) of HMA) using a layer coefficient (a) that represents the relative strength of the construction materials in that layer. Additionally, all layers below the HMA layer are assigned a drainage coefficient (m) that represents the relative loss of strength in a layer due to its drainage characteristics and the total time it is exposed to near-saturation moisture conditions. Generally, quick-draining layers that almost never become saturated can have coefficients as high as 1.4 while slow-draining layers that are often saturated can have drainage coefficients as low as 0.40. Keep in mind that a drainage coefficient is basically a way of making a specific layer thicker. If a fundamental drainage problem is suspected, thicker layers may only be of marginal benefit – a better solution is to address the actual drainage problem by using very dense layers (to minimize water infiltration) or designing a drainage system. Because of the peril associated with its use, often times the drainage coefficient is neglected (i.e., set as m = 1.0).
- Serviceable life. The difference in present serviceability index (PSI) between construction and end-of-life is the serviceability life. The equation compares this to default values of 4.2 for the immediately-after-construction value and 1.5 for end-of-life (terminal serviceability). Typical values used now are:
- Post-construction: 4.0 – 5.0 depending upon construction quality, smoothness, etc.
- End-of-life (called “terminal serviceability”): 1.5 – 3.0 depending upon road use (e.g., interstate highway, urban arterial, residential)
- Subgrade support. Subgrade support is characterized by the subgrade’s resilient modulus(MR). Intuitively, the amount of structural support offered by the subgrade should be a large factor in determining the required pavement structure.
Outputs
The 1993 AASHTO Guide equation can be solved for any one of the variables as long as all the others are supplied. Typically, the output is either total ESALs or the required Structural Number (or the associated pavement layer depths). To be most accurate, the flexible pavement equation described in this chapter should be solved simultaneously with the flexible pavement ESAL equation. This solution method is an iterative process that solves for ESALs in both equations by varying the Structural Number. It is iterative because the Structural Number (SN) has two key influences:
- The Structural Number determines the total number of ESALs that a particular pavement can support. This is evident in the flexible pavement design equation presented in this section.
- The Structural Number also determines what the 80 kN (18,000 lb.) ESAL is for a given load.
Therefore, the Structural Number is required to determine the number of ESALs to design for before the pavement is ever designed. The iterative design process usually proceeds as follows:
- Determine and gather flexible pavement design inputs (ZR, So, ΔPSI and MR).
- Determine and gather flexible pavement ESAL equation inputs (Lx, L2x, G).
- Assume a Structural Number (SN).
- Determine the equivalency factor for each load type by solving the ESAL equation using the assumed SN for each load type.
- Estimate the traffic count for each load type for the entire design life of the pavement and multiply it by the calculated ESAL to obtain the total number of ESALs expected over the design life of the pavement.
- Insert the assumed SN into the design equation and calculate the total number of ESALs that the pavement will support over its design life.
- Compare the ESAL values in #5 and #6. If they are reasonably close (say within 5 percent) use the assumed SN. If they are not reasonably close, assume a different SN, go to step #4 and repeat the process.
In practice, the flexible pavement design equation is usually solved independently of the ESAL equation by using an ESAL value that is assumed independent of structural number. Although this assumption is not true, pavement structure depths calculated using it are reasonably accurate. This design process usually proceeds as follows:
- Assume a structural number (SN) for ESAL calculations. Although often not overtly stated, a structural number must be assumed in order to calculate ESALs.
- Determine the load equivalency factor (LEF) for each load type by solving the ESAL equation using the assumed SN for each load type. Typically, a standard set of load types is used (e.g., single unit trucks, tractor-trailer trucks and buses).
- Estimate the traffic count for each load type for the entire design life of the pavement and multiply it by the calculated LEF to obtain the total number of ESALs expected over the design life of the pavement.
- Determine and gather flexible pavement design inputs (ZR, So, ΔPSI and MR).
- Solve the design equation for SN.
- Check to see that the computed SN value is reasonably close to that assumed for ESAL calculations. This step of often neglected.
Design Utility
This design utility solves the 1993 AASHTO Guide basic design equation for flexible pavements. It also supplies some basic information on variable descriptions, typical values and equation precautions.
1993 AASHTO Flexible Pavement Structural Design
- AASHTO Guide for Design of Pavement Structures. American Association of State Highway and Transportation Officials. Washington, D.C.↵
