The main empirical portions of the mechanistic-empirical design process are the equations used to compute the number of loading cycles to failure. These equations are derived by observing the performance of pavements and relating the type and extent of observed failure to an initial strain under various loads. Currently, two types of failure criteria are widely recognized, one relating to fatigue cracking and the other to rutting initiating in the subgrade. A third deflection-based criterion may be of use in special applications. Note that since these failure criteria are empirically established, they must be calibrated to specific local conditions and are generally not applicable on a national scale.
Fatigue Failure Criterion
Many equations have been developed to estimate the number of repetitions to failure in the fatigue mode for asphalt concrete. Most of these rely on the horizontal tensile strain at the bottom of the HMA layer (εt) and the elastic modulus of the HMA. One commonly accepted criterion developed by Finn et al. (1977[1]) is:
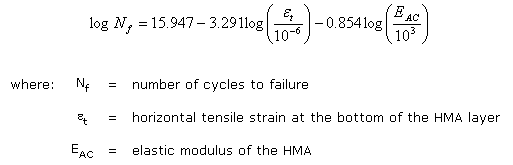
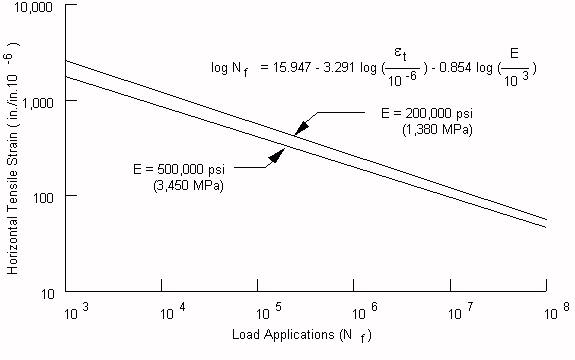
The above equation defines failure as fatigue cracking over 10 percent of the wheelpath area. Figure 1 shows the relationship between tensile strain in the asphalt concrete and the number of cycles to failure for two levels of asphalt concrete elastic modulus. This relationship assumes bottom-up cracking rather than top-down cracking.
Rutting Failure Criterion
Rutting can initiate in any layer of the structure, making it more difficult to predict than fatigue cracking. Current failure criteria are intended for rutting that can be attributed mostly to a weak pavement structure. This is typically expressed in terms of the vertical compressive strain (εv) at the top of the subgrade layer:
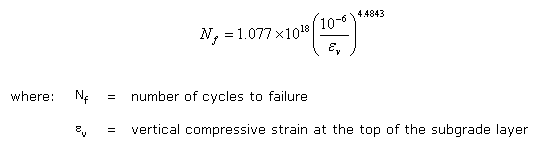
The above equation defines failure as 12.5 mm (0.5-inch) depressions in the wheelpaths of the pavement. Figure 2 illustrates how the vertical compressive strain relates to the number of cycles to failure.
2. Limiting subgrade strain criterion for rutting.
Deflection Failure Criterion
A number of deflection based criteria have been developed by various agencies over the last 40 years or so. The AASHO Road Test and Roads and Transportation Association of Canada (RTAC) criteria are shown here. Both these criteria were developed based on spring seasonal deflections.
AASHO Road Test Criterion
The AASHO Road Test results were used to develop the following relations (Highway Research Board, 1962b[2]):
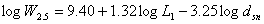
| where: | W2.5 | equals | number of applications of axle load L1 sustained by the pavement to a terminal serviceability index of 2.5 |
|---|---|---|---|
| L1 | equals | single axle load (kips) | |
| dsn | equals | Benkelman Beam springtime measured pavement surface deflection (0.001 in.) measured at the AASHO Road Test (Spring 1959) after “disappearance of frost.” |
This criterion was based on data from Loops 2 through 6 and single axle loads of 6, 12, 18, 22.4, and 30 kips (1 kip = 1,000 lbs.). The following equation is obtained if L1 = 18,000 lbs. (a standard ESAL):
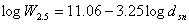
Roads and Transportation Association of Canada (RTAC) Criterion
The RTAC criterion can be calculated as follows (after RTAC (1977[3]) and Haas et al. (1994[4])):

Table 1 shows the limiting deflections for both criteria:
Table 1. Limiting Deflections
| Loads to Failure | Limiting "Spring" Deflection (in.) | |
| AASHO Road Test | RTAC | |
| 10,000 | 0.148 | 0.100 |
| 100,000 | 0.072 | 0.080 |
| 1,000,000 | 0.036 | 0.040 |
| 10,000,000 | 0.018 | 0.020 |
- The Use of Distress Prediction Subsystems for the Design of Pavement Structures. Proceedings, 4th International Conference on the Structural Design of Asphalt Pavements, University of Michigan. Ann Arbor, MI.↵
- The AASHO Road Test: Report 5, Pavement Research. Special Report 61E. Highway Research Board, National Academy of Sciences. Washington, D.C.↵
- Pavement Management Guide. Roads and Transportation Association of Canada. Ottawa, Canada.↵
- Modern Pavement Management. Krieger Publishing Company. Malabar, FL.↵
