In CRCP and JRCP, reinforcing steel is used to hold tightly together any cracks that may form. Cracks formation depends upon temperature, moisture and base material friction. As the slab cools and loses moisture, it will contract. This contraction is resisted by friction with the base material. If this frictional force becomes greater than the tensile strength of the PCC, the slab will crack and the tensile stresses will be transferred to the embedded reinforcing steel. Thus, in order to prevent excessive crack widths, the reinforcing steel must be designed to accommodate these stresses without significant elongation. The amount of steel is typically expressed as a percentage of the slab cross sectional area. This section, taken largely from the 1993 AASHTO Guide, briefly discusses the design process for JRCP and CRCP.
JRCP Reinforcing Steel Design
JRCP reinforcing steel design is a straightforward process that depends on the following three factors:
- Slab length. This has a large effect on the maximum PCC tensile stresses developed within the slab. As the slab length increases, the contact area with the base material increases, which increases the total resisting frictional force, resulting in higher tensile stresses as the slab contracts and/or loses moisture.
- Steel working stress. This is usually taken to be 75% of the steel yield stress. The steel working stress must be great enough to resist the frictional forces developed during slab contraction.
- Friction factor. This represents the frictional resistance between the bottom of the slab and the top of the base material. It is like a coefficient of friction. Table 1 shows the 1993 AASHTO Guide recommended frictional factors.
Table 1. Recommended Friction Factors (from McCullough, 1966 as referenced in AASHTO, 1993[1])
| Type of Material Beneath the Slab | Friction Factor (F) |
|---|---|
| Surface Treatment | 2.2 |
| Lime Stabilization | 1.8 |
| Asphalt Stabilization | 1.8 |
| Cement Stabilization | 1.8 |
| River Gravel | 1.5 |
| Crushed Stone | 1.5 |
| Sandstone | 1.2 |
| Natural Subgrade | 0.9 |
Taking the above three factors into account, the following equation is used to determine the amount of reinforcing steel as a percentage of slab cross-sectional area:
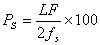
| where: | L | = | slab length |
| F | = | friction factor | |
| fs | = | steel working stress (usually taken as 75% of the yield stress) |
This JRCP design procedure is also used to design CRCP transverse reinforcing steel.
CRCP Reinforcing Steel Design
CRCP reinforcing steel design is used to determine the amount of longitudinal steel that will satisfy the following three limiting criteria:
- Crack spacing. To minimize crack spalling, the maximum spacing between cracks should be less than 2.5 m (8 ft.). To minimize the potential for punchouts, the minimum spacing between cracks should be 1.07 m (3.5 ft.).
- Crack width. To minimize spalling and water penetration, the allowable crack width should not exceed 1 mm (0.04 inches). Small crack widths are essential to CRCP performance.
- Steel stress. This is usually taken to be 75% of the steel yield stress to prevent any plastic deformation, although studies have shown that many CRCP pavements have performed adequately even though their steel stress was calculated to be above yield stress (Majidzadeh, 1978 as referenced in AASHTO, 1993[1]).
One longitudinal steel design procedure is given by the 1993 AASHTO Guide:
- Solve the following three limiting criteria equations for the percentage of steel required (yes, they appear difficult, but the 1993 AASHTO Guide contains nomograph solutions). Note that crack spacing (x) should be solved using input values of x = 2.5 m (8 ft.) to determine a minimum amount of steel required to keep the maximum crack spacing less than 2.5 m (8 ft.), and x = 1.07 m (3.5 ft.) to determine a maximum amount of steel required to keep the minimum crack spacing greater than 1.07 m (3.5 ft.). Crack width and steel working stress solutions will give a minimum amount of required steel.

| where: | ft | = | PCC tensile stress at 28 days |
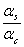 |
= | ratio of the steel thermal coefficient (5 x 10-6 in./in./°F) to PCC thermal coefficient | |
| φ | = | steel bar diameter | |
| σw | = | wheel load stress | |
| P | = | cross-sectional amount of steel as a percentage of cross-sectional slab area | |
| Z | = | PCC shrinkage coefficient | |
| ΔT | = | design temperature drop (between high and low expected temperatures) |
- The solutions to step 1 will provide the minimum (Pmin) and maximum (Pmax) required percentage of reinforcing steel. If Pmax > Pmin then the design is feasible and can continue. If not, the design inputs need to be modified and the above equations recalculated.
- Determine the number (N) of reinforcing bars required:
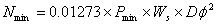 |
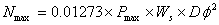 |
| where: | Pmin | = | minimum steel percentage |
| Pmax | = | maximum steel percentage | |
| Ws | = | total width of pavement section | |
| D | = | slab thickness | |
| φ | = | reinforcing bar or wire diameter |
- Determine the design number of reinforcing bars (Ndesign) such that it is a whole number between Nmin and Nmax.
Transverse steel can then be designed using the JRCP procedure to define the amount of steel required and the following equation to determine the reinforcing bar spacing:
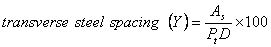
| where: | As | = | cross-sectional area of transverse reinforcing steel |
| Pt | = | cross-sectional amount of transverse steel as a percentage of cross-sectional slab area | |
| D | = | slab thickness |
- AASHTO Guide for Design of Pavement Structures. American Association of State Highway and Transportation Officials. Washington, D.C.↵


