Design a new flexible pavement for a major interstate highway using the following conditions (four lanes each direction):
| Pavement location: | Urban |
| Pavement functional classification: | Interstate |
| Number of lanes: | 3 lanes in each direction |
| Traffic distribution: | Assume 80% of the loading occurs in the design lane |
| Annual growth rate: | Assume 2% |
| Design period: | Investigate 20, 30 and 40 year design periods |
| Construction Materials: | Surface course: 12.5 mm (0.5 inch) Superpave with E = 3,447 MPa (500,000 psi)Binder course: Dense-graded HMA mix with a nominal maximum aggregate sizeof 25 mm (1 inch). Use E = 3,447 MPa (500,000 psi)Base course: Crushed aggregate with MR= 193 MPa (28,000 psi)Subbase course: None used |
| Subgrade: | MR = 103 MPa (15,000 psi) in the dry months of May through October MR = 86 MPa (12,500 psi) in the wet months of November through April |
| Overall serviceability loss: | po – pt = 4.5 – 3.0 = 1.5 |
| Reliability: | Investigate three levels: R = 90%, R = 95%, R = 99%. This represents a typical range of reliability levels encountered for Interstate highways. |
| So: | 0.50 |
| Traffic count: | Single unit trucks (assume 0.40 ESALs per truck) = 1872/day |
| Double unit trucks (assume 1.00 ESALs per truck) = 1762/day | Double unit trucks (assume 1.00 ESALs per truck) = 1762/day |
| Truck trains – trucks with more than 2 units (assume 1.75 ESALs per truck) = 247/day | Truck trains – trucks with more than 2 units (assume 1.75 ESALs per truck) = 247/day |
Solution
By looking at several different design periods and reliability levels this example gives an idea of the relative influence of these inputs. Work can be verified by using the Flexible Pavement Structural Design Utility.
ESALs per year
This step involves converting the daily traffic volume into an annual ESAL amount. Pavements are typically designed for the critical lane or “design lane”, which accounts for traffic distribution.
ESALs per year = (Vehicles/day) (Lane Distribution Factor) (days/yr) (ESALs/Vehicle)
| Singles: | (1872/day) (0.8) (365) (0.40) | equals | 218,650 ESALs/yr |
| Doubles: | (762/day) (0.8) (365) (1.00) | equals | 514,504 ESALs/yr |
| Trains: | (247/day) (0.8) (365) (1.75) | equals | 126,217 ESALs/yr |
| Total | equals | 859,371 ESALs/yr | |
| Rounded total | equals | 860,000 ESALs/yr |
Design ESALs
The standard multiplier to calculate compound growth is:
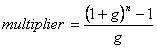
| 20 year design life: | 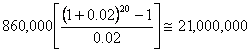 |
| 30 year design life: | 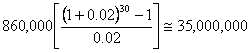 |
| 40 year design life: | 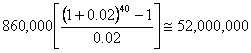 |
Calculate the Effective Subgrade Support
Note that in this example there are two different values of subgrade resilient modulus given: one for dry months and one for wet months. Realistically, subgrade support varies even more than this simplistic assumption, however, the same method for estimating a design subgrade resilient modulus can be used for more precise assumptions. The standard method in the 1993 AASHTO Guide for Design of Pavement Structures involves calculating a weighted average subgrade resilient modulus based on the relative pavement damage. Because lower values of subgrade resilient modulus result in more pavement damage, lower values of subgrade resilient modulus are weighted more heavily. The relative damage equation used in the 1993 AASHTO Guide for Design of Pavement Structures is:
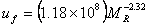
| where: | uf | equals | relative damage factor |
| MR | equals | resilient modulus in psi |
Therefore, over an entire year the calculations would be:
| Month | MR | uf |
| January | 86 MPa (12,500 psi) | 0.037 |
| February | 86 MPa (12,500 psi) | 0.037 |
| March | 86 MPa (12,500 psi) | 0.037 |
| April | 86 MPa (12,500 psi) | 0.037 |
| May | 103 MPa (15,000 psi) | 0.024 |
| June | 103 MPa (15,000 psi) | 0.024 |
| July | 103 MPa (15,000 psi) | 0.024 |
| August | 103 MPa (15,000 psi) | 0.024 |
| September | 103 MPa (15,000 psi) | 0.024 |
| October | 103 MPa (15,000 psi) | 0.037 |
| November | 86 MPa (12,500 psi) | 0.037 |
| December | 86 MPa (12,500 psi) | 0.037 |
| average relative damage | equals |
| Rearrange the relative damage equation and get |
Use the 1993 AASHTO Empirical Equation
Using the previously calculated ESAL results and the 1993 flexible pavement structural design equiation the following pavement thickness designs can be calculated:
| Design Period | Design Period ESALs | Pavement Layer | Layer Thickness | ||
| Reliability = 90% | Reliability = 95% | Reliability = 99% | |||
| 20 years | <21,000,000 | HMA Surface Course | 105 mm (4.2 inches) |
105 mm (4.2 inches) |
105 mm (4.2 inches) |
| HMA Binder Course | 130 mm (5.1 inches) |
150 mm (5.8 inches) |
180 mm (7.21 inches) |
||
| Base Course | 135 mm (5.4 inches) |
135 mm (5.4 inches) |
135 mm (5.4 inches) |
||
| SN | 4.79 | 5.10 | 5.70 | ||
| <30 years | <35,000,000 | HMA Surface Course | 105 mm (4.2 inches) |
105 mm (4.2 inches) |
105 mm (4.2 inches) |
| HMA Binder Course | 150 mm (6.0 inches) |
170 mm (6.7 inches) |
205 mm (8.1 inches) |
||
| Base Course | 135 mm (5.4 inches) |
135 mm (5.4 inches) |
135 mm (5.4 inches) |
||
| SN | 5.17 | 5.49 | 6.11 | ||
| <40 years | <52,000,000 | HMA Surface Course | 105 mm (4.2 inches) |
105 mm (4.2 inches) |
105 mm (4.2 inches) |
| HMA Binder Course | 170 mm (6.6 inches) |
190 mm (7.4 inches) |
225 mm (8.8 inches) |
||
| Base Course | 135 mm (5.4 inches) |
135 mm (5.4 inches) |
135 mm (5.4 inches) |
||
| SN | 5.47 | 5.80 | 6.44 | ||
| Layer coefficients used were 0.44 for HMA and 0.13 for crushed stone | |||||
| Frost design requirements must be checked if subgrade soil frost susceptible | |||||
In this particular example, which only shows one set of possible solutions, the HMA surface course and base course layer depths were kept constant and the HMA binder course depth was varied depending upon requirements. Notice also that a change in reliability level from 90% to 99% results in a SN increase of about 1.0 and a resultant increase in HMA thickness of about 55 mm (2 inches). It is interesting to note that in most empirical design procedures HMA, no matter what the specific mix designation or size, is treated equally. Here, the 12.5 mm (0.5 inch) Superpave surface course and the 25 mm (1 inch) dense-graded binder course are structurally equivalent.
