At first glance, this equation looks quite complex – it is.

| Where: | W | = | axle applications inverse of equivalency factors (where W18 = number of 18,000 lb (80 kN) single axle loads) |
| Lx | = | axle load being evaluated (kips) | |
| L18 | = | 18 (standard axle load in kips) | |
| L2 | = | code for axle configuration 1 = single axle 2 = tandem axle 3 = triple axle (added in the 1986 AASHTO Guide) x = axle load equivalency factor being evaluated s = code for standard axle = 1 (single axle) |
|
| G | = | 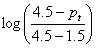 a function of the ratio of loss in serviceability at time, t, to the potential loss taken at a point where pt = 1.5 a function of the ratio of loss in serviceability at time, t, to the potential loss taken at a point where pt = 1.5 |
|
| pt | = | “terminal” serviceability index (point at which the pavement is considered to be at the end of its useful life) | |
| b | = | 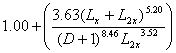 function which determines the relationship between serviceability and axle load applications function which determines the relationship between serviceability and axle load applicationsD = Slab Depth in inches |
Example Calculation
- Assumptions: Single axle, 30,000 lb (133 kN), D = 7 in., pt = 2.5
- Answer: (Table D.13, p. D-15, 1993 AASHTO Guide) = 7.7
- Calculations
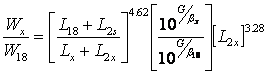
| where : | W18 | = | predicted number of 18,000 lb (80 kN) single axle load applications |
| W30 | = | predicted number of 30,000 lb (133 kN) single axle load applications | |
| Lx | = | L30 = 30 | |
| L2x | = | 1 (single axle) | |
| G | = | serviceability loss factor | |
| = | 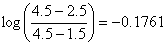 |
||
| b30 | = | curve slope factor | |
| = | 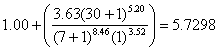 |
||
| and | G/b30 | = | -0.1761/5.7298 = -0.03073 |
| b18 | = | 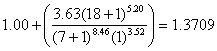 |
|
| G/b18 | = | -0.1761/1.3709 = -0.12845 | |
| Thus, | 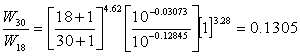 |
||
| and | 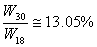 of W18 loads allowable with a 30,000 lb. single axle of W18 loads allowable with a 30,000 lb. single axle |
||
| Finally, | LEF | = | 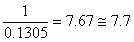 (same as contained in 1993 AASHTO Guide âcol Appendix D) (same as contained in 1993 AASHTO Guide âcol Appendix D) |
