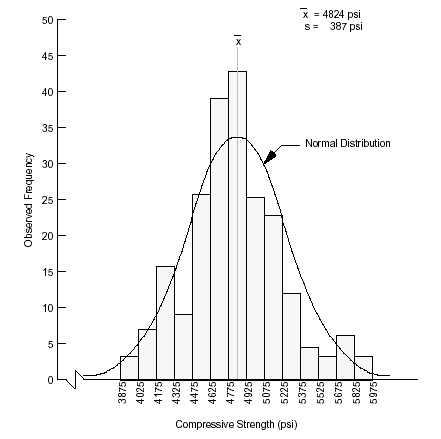
The normal distribution is a data distribution that can be used to describe many types of measurements in engineering. Basically, a normal distribution is a bell shaped curve. Figure 1 illustrates a bell curve, superimposed over a histogram of PCC compressive strength data. Such a distribution is very convenient to use because it is characterized by the mean (μ or x) and standard deviation (σ or s).
As Figure 1 shows, most of the strength measurements cluster around the mean (x = 4,824 psi), while fewer measurements are near the lowest (3,875 psi) and highest (5,975 psi) strength values. The theoretical normal distribution extends out infinitely in both directions and never quite reaches the horizontal axis and has a total area under the curve of 1.00 (i.e., 100 percent of the data values are represented by the distribution). Since it extends indefinitely in either direction (minus infinity to plus infinity), it encompasses all of the results that can occur. The area under the curve within these two limits must therefore be equal to unity (i.e., 1.000 or 100 percent). For practical purposes, however, most of the data values (99.73 percent) occur within 3σ of the mean. A far more important result than those mentioned above is also related to the fact that the area under the curve is equal to 100 percent. Because of this, it can be stated that the probability of finding a data value between any two values of x is equal to the area under the normal distribution between those values.
The Normal Distribution Equation
The height of a normal distribution (y) can be defined by its corresponding value of x (refer to Figure 2) by the following equation:

Example
Based on hypothetical density data results, calculate the area under the normal curve between 105 and 115 lb/ft3 for a standard deviation of 5 lb/ft3. These calculations are:
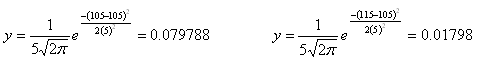
 To determine such probabilities in this manner is tedious and time consuming. There is an easier way to determine these probabilities than computing and tabulating y’s for various means and standard deviations. To do this, you must convert the normal distribution to a standard normal distribution and define a variable “z,” which is:
To determine such probabilities in this manner is tedious and time consuming. There is an easier way to determine these probabilities than computing and tabulating y’s for various means and standard deviations. To do this, you must convert the normal distribution to a standard normal distribution and define a variable “z,” which is:
![]()
If you substitute z into the normal distribution equation, the following relationship results:
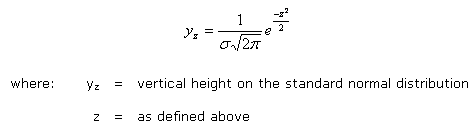
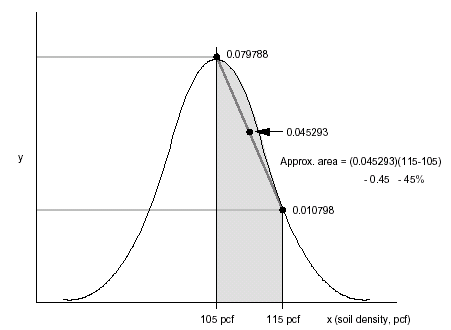
Refer to Figure 3, which illustrates this important transformation. Thus, you can see that the probability of having a density test between 105 and 115 pcf is about 47.7 percent (or 34.1 + 13.6 percent).
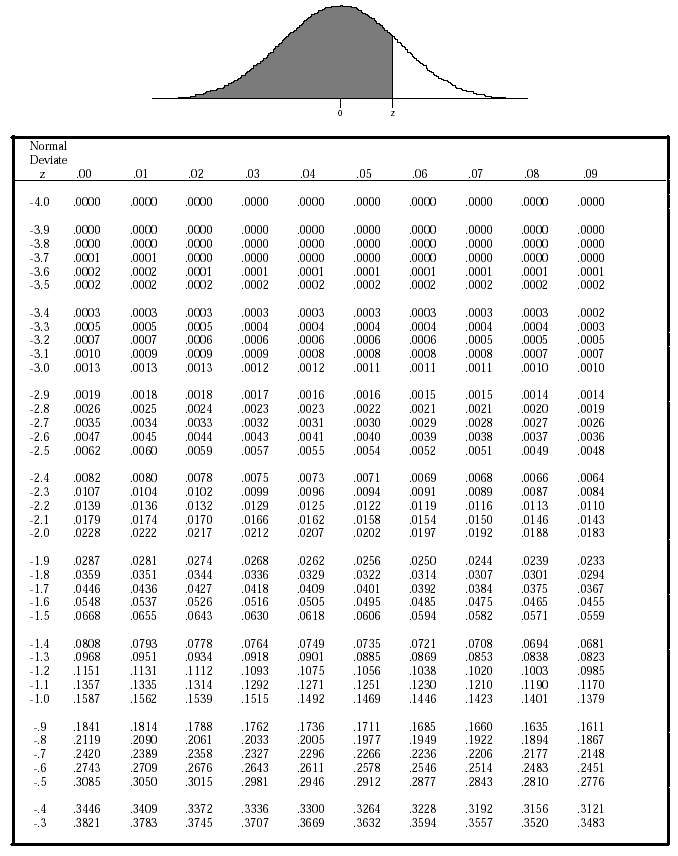
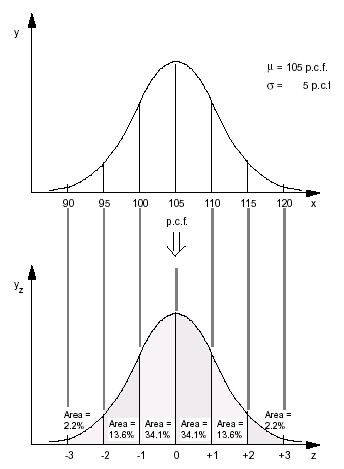 Fortunately, the “z-statistic” has been published in tables to allow for easy computation. Such a table is shown as Table 1. You can see that:
Fortunately, the “z-statistic” has been published in tables to allow for easy computation. Such a table is shown as Table 1. You can see that:
- mean ± 1 standard deviations @ 68.2% of area
- mean ± 2 standard deviations @ 95.4% of area
- mean ± 3 standard deviations @ 99.8% of area
Recall that all of the area under a normal distribution is 100% and the values above correspond to the z-statistic.
Table 1: Normal Distribution Table (from Ulberg, 1987[1])
- Highway Research Manual. Draft Final Report, Research Project Y3399, Task 29, Washington State Department of Transportation. Olympia, WA.↵
